Portal:Mathematics

• 
  Abacus, a ancient hand-operated calculating.
• 
  Portrait of Emmy Noether, around 1900.
• 
  Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

• 

  

  The manipulations of the Rubik's Cube form the Rubik's Cube group.

  
  
  In mathematics, a group is a set with an operation that associates every pair of elements of the set to an element of the set—also known as a binary operation—that satisfies the following properties:

  1. The operation is associative.
  2. The operation has an identity element.
  3. Every element of the set has an inverse element.

  
  
  Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called ⁠$1$⁠ (these properties characterize the integers in a unique way). (Full article...)
• 
  General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever is
  present matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations.
  
  Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...)
• 
  
  

  

  Cantor, c. 1910

  
  Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.
  
  Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)
• 
  
  

  

  Portrait by August Köhler, c. 1910, after 1627 original

  
  Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ^ⓘ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.
  
  Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
  Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
• 
  
  

  

  Title page of the first edition of Wright's Certaine Errors in Navigation (1599)

  
  Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.
  
  Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)
• 
  In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.
  
  The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...)
• 
  
  

  

  Kaczynski after his arrest in 1996

  
  Theodore John Kaczynski (/kəˈzɪnski/ ^ⓘ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ ^ⓘ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle.
  
  Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored Industrial Society and Its Future, a 35,000-word manifesto and social critique opposing all forms of technology, rejecting leftism, and advocating a nature-centered form of anarchism. (Full article...)
• 
  
  

  

  A stamp of Zhang Heng issued by China Post in 1955

  
  Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Eastern Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.
  
  Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...)
• 
  
  

  

  Portrait by Jakob Emanuel Handmann, 1753

  
  Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] ^ⓘ, Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.
  
  Euler is credited for popularizing the Greek letter $\pi$ (lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation $f(x)$ for the value of a function, the letter $i$ to express the imaginary unit ${\sqrt {-1}}$, the Greek letter $\Sigma$ (capital sigma) to express summations, the Greek letter $\Delta$ (capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant $e$, the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...)
• 
  
  

  

  Rejewski, c. 1932

  
  Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ^ⓘ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.
  
  Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
• 
  
  

  

  One of Molyneux's celestial globes, which is displayed in Middle Temple Library – from the frontispiece of the Hakluyt Society's 1889 reprint of A Learned Treatise of Globes, both Cœlestiall and Terrestriall, one of the English editions of Robert Hues' Latin work Tractatus de Globis (1594)

  
  Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.
  
  Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...)
• 
  
  

  

  Noether c. 1900–1910

  
  Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She proved Noether's first and second theorems, which are fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.
  
  Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
• 
  
  

  

  Hilary Putnam

  
  The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.
  
  Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
• 

  

  Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).

  
  
  In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
  It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
  and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.
  
  The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)
• 

  

  The weighing pans of this balance scale contain zero objects, divided into two equal groups.

  
  In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
  
  Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)

Good articles

• 

  

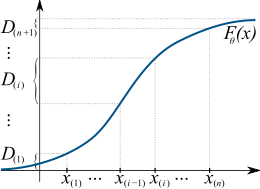
  The maximum spacing method tries to find a distribution function such that the spacings, D_(i), are all approximately of the same length. This is done by maximizing their geometric mean.

  
  
  In statistics, maximum spacing estimation (MSE or MSP), or maximum product of spacing estimation (MPS), is a method for estimating the parameters of a univariate statistical model. The method requires maximization of the geometric mean of spacings in the data, which are the differences between the values of the cumulative distribution function at neighbouring data points.
  
  The concept underlying the method is based on the probability integral transform, in that a set of independent random samples derived from any random variable should on average be uniformly distributed with respect to the cumulative distribution function of the random variable. The MPS method chooses the parameter values that make the observed data as uniform as possible, according to a specific quantitative measure of uniformity. (Full article...)
• 

  

  Rule 184, run for 128 steps from random configurations with each of three different starting densities: top 25%, middle 50%, bottom 75%. The view shown is a 300-pixel crop from a wider simulation.

  
  Rule 184 is a one-dimensional binary cellular automaton rule, notable for solving the majority problem as well as for its ability to simultaneously describe several, seemingly quite different, particle systems:
  

  • Rule 184 can be used as a simple model for traffic flow in a single lane of a highway, and forms the basis for many cellular automaton models of traffic flow with greater sophistication. In this model, particles (representing vehicles) move in a single direction, stopping and starting depending on the cars in front of them. The number of particles remains unchanged throughout the simulation. Because of this application, Rule 184 is sometimes called the "traffic rule".
  • Rule 184 also models a form of deposition of particles onto an irregular surface, in which each local minimum of the surface is filled with a particle in each step. At each step of the simulation, the number of particles increases. Once placed, a particle never moves.
  • Rule 184 can be understood in terms of ballistic annihilation, a system of particles moving both leftwards and rightwards through a one-dimensional medium. When two such particles collide, they annihilate each other, so that at each step the number of particles remains unchanged or decreases.

  
  The apparent contradiction between these descriptions is resolved by different ways of associating features of the automaton's state with particles. (Full article...)
• 
  In control system theory, and various branches of engineering, a transfer function matrix, or just transfer matrix is a generalisation of the transfer functions of single-input single-output (SISO) systems to multiple-input and multiple-output (MIMO) systems. The matrix relates the outputs of the system to its inputs. It is a particularly useful construction for linear time-invariant (LTI) systems because it can be expressed in terms of the s-plane.
  
  In some systems, especially ones consisting entirely of passive components, it can be ambiguous which variables are inputs and which are outputs. In electrical engineering, a common scheme is to gather all the voltage variables on one side and all the current variables on the other regardless of which are inputs or outputs. This results in all the elements of the transfer matrix being in units of impedance. The concept of impedance (and hence impedance matrices) has been borrowed into other energy domains by analogy, especially mechanics and acoustics. (Full article...)
• 
  The Math Myth: And Other STEM Delusions is a 2016 nonfiction book by Queens College political scientist Andrew Hacker analyzing and critiquing the United States educational system's teaching of mathematics as a linear progression towards more advanced fields. Based on a 2012 New York Times op-ed by Hacker titled "Is Algebra Necessary", Hacker argues that the teaching of advanced algebra, trigonometry, and calculus is not useful to the majority of students. He further claims that the requirement of advanced mathematics courses in secondary education contributes to dropout rates and impedes socioeconomically disadvantaged students from pursuing further education. Hacker critiques the Common Core system and American focus on STEM education in lieu of social sciences, arguing that the educational system should prioritize numeracy over pure mathematics education.
  
  The Math Myth received broadly critical coverage from critics and mathematicians, some citing Hacker's arguments as "disingenuous" and contributing to an elitist attitude towards mathematics, with many citing a lack of exploration on mathematics in early childhood and primary education. Others praised Hacker's work, describing the book as offering a convincing critique of STEM education in the United States and empowering to students struggling in mathematics. (Full article...)
• 
  
  

  

  Graham in 1998

  
  Ronald Lewis Graham (October 31, 1935 – July 6, 2020) was an American mathematician credited by the American Mathematical Society as "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years". He was president of both the American Mathematical Society and the Mathematical Association of America, and his honors included the Leroy P. Steele Prize for lifetime achievement and election to the National Academy of Sciences.
  
  After graduate study at the University of California, Berkeley, Graham worked for many years at Bell Labs and later at the University of California, San Diego. He did important work in scheduling theory, computational geometry, Ramsey theory, and quasi-randomness, and many topics in mathematics are named after him. He published six books and about 400 papers, and had nearly 200 co-authors, including many collaborative works with his wife Fan Chung and with Paul Erdős. (Full article...)
• 

  

  In this example, the alternating sum of angles (clockwise from the bottom) is 90° − 45° + 22.5° − 22.5° + 45° − 90° + 22.5° − 22.5° = 0°. Since it adds to zero, the crease pattern may be flat-folded.

  
  Kawasaki's theorem or Kawasaki–Justin theorem is a theorem in the mathematics of paper folding that describes the crease patterns with a single vertex that may be folded to form a flat figure. It states that the pattern is flat-foldable if and only if alternatingly adding and subtracting the angles of consecutive folds around the vertex gives an alternating sum of zero.
  Crease patterns with more than one vertex do not obey such a simple criterion, and are NP-hard to fold.
  
  The theorem is named after one of its discoverers, Toshikazu Kawasaki. However, several others also contributed to its discovery, and it is sometimes called the Kawasaki–Justin theorem or Husimi's theorem after other contributors, Jacques Justin and Kôdi Husimi. (Full article...)
• 

  

  Wave functions of the electron in a hydrogen atom at different energy levels. Quantum mechanics cannot predict the exact location of a particle in space, only the probability of finding it at different locations. The brighter areas represent a higher probability of finding the electron.

  
  Quantum mechanics is a fundamental theory that describes the behavior of nature at and below the scale of atoms. It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science.
  
  Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation, valid at large (macroscopic/microscopic) scale. (Full article...)
• 

  

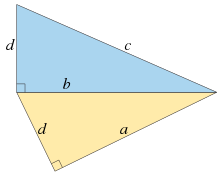
  Two right triangles with the two legs of the top one equal to the leg and hypotenuse of the bottom one. For these lengths, $a^{2}$, $b^{2}$, and $c^{2}$ form an arithmetic progression separated by a gap of $d^{2}$. It is not possible for all four lengths $a$, $b$, $c$, and $d$ to be integers.

  
  Fermat's right triangle theorem is a non-existence proof in number theory, published in 1670 among the works of Pierre de Fermat, soon after his death. It is the only complete proof given by Fermat. It has many equivalent formulations, one of which was stated (but not proved) in 1225 by Fibonacci. In its geometric forms, it states:

  • A right triangle in the Euclidean plane for which all three side lengths are rational numbers cannot have an area that is the square of a rational number. The area of a rational-sided right triangle is called a congruent number, so no congruent number can be square.
  • A right triangle and a square with equal areas cannot have all sides commensurate with each other.
  • There do not exist two integer-sided right triangles in which the two legs of one triangle are the leg and hypotenuse of the other triangle.

  
  More abstractly, as a result about Diophantine equations (integer or rational-number solutions to polynomial equations), it is equivalent to the statements that:

  • If three square numbers form an arithmetic progression, then the gap between consecutive numbers in the progression (called a congruum) cannot itself be square.
  • The only rational points on the elliptic curve $y^{2}=x(x-1)(x+1)$ are the three trivial points with $x\in \{-1,0,1\}$ and $y=0$.
  • The quartic equation $x^{4}-y^{4}=z^{2}$ has no nonzero integer solution.

  
  An immediate consequence of the last of these formulations is that Fermat's Last Theorem is true in the special case that its exponent is 4. (Full article...)
• 

  

  The main arithmetic operations are addition, subtraction, multiplication, and division.

  
  
  Arithmetic is an elementary branch of mathematics that studies numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.
  
  Arithmetic systems can be distinguished based on the type of numbers they operate on. Integer arithmetic is about calculations with positive and negative integers. Rational number arithmetic involves operations on fractions of integers. Real number arithmetic is about calculations with real numbers, which include both rational and irrational numbers. (Full article...)
• 
  Klaus Friedrich Roth FRS (29 October 1925 – 10 November 2015) was a German-born British mathematician who won the Fields Medal for proving Roth's theorem on the Diophantine approximation of algebraic numbers. He was also a winner of the De Morgan Medal and the Sylvester Medal, and a Fellow of the Royal Society.
  
  Roth moved to England as a child in 1933 to escape the Nazis, and was educated at the University of Cambridge and University College London, finishing his doctorate in 1950. He taught at University College London until 1966, when he took a chair at Imperial College London. He retired in 1988. (Full article...)
• 

  

  A homomorphism from the flower snark J₅ into the cycle graph C₅.
  It is also a retraction onto the subgraph on the central five vertices. Thus J₅ is in fact homo­mor­phi­cally equivalent to the core C₅.

  
  In the mathematical field of graph theory, a graph homomorphism is a mapping between two graphs that respects their structure. More concretely, it is a function between the vertex sets of two graphs that maps adjacent vertices to adjacent vertices.
  
  Homomorphisms generalize various notions of graph colorings and allow the expression of an important class of constraint satisfaction problems, such as certain scheduling or frequency assignment problems.
  The fact that homomorphisms can be composed leads to rich algebraic structures: a preorder on graphs, a distributive lattice, and a category (one for undirected graphs and one for directed graphs).
  The computational complexity of finding a homomorphism between given graphs is prohibitive in general, but a lot is known about special cases that are solvable in polynomial time. Boundaries between tractable and intractable cases have been an active area of research. (Full article...)
• 

  

  A 1-forest (a maximal pseudoforest), formed by three 1-trees

  
  In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be connected to each other by a path of consecutive edges. A pseudotree is a connected pseudoforest.
  
  The names are justified by analogy to the more commonly studied trees and forests. (A tree is a connected graph with no cycles; a forest is a disjoint union of trees.) Gabow and Tarjan attribute the study of pseudoforests to Dantzig's 1963 book on linear programming, in which pseudoforests arise in the solution of certain network flow problems. Pseudoforests also form graph-theoretic models of functions and occur in several algorithmic problems. Pseudoforests are sparse graphs – their number of edges is linearly bounded in terms of their number of vertices (in fact, they have at most as many edges as they have vertices) – and their matroid structure allows several other families of sparse graphs to be decomposed as unions of forests and pseudoforests. The name "pseudoforest" comes from Picard & Queyranne (1982). (Full article...)

Did you know

• ... that people in Madagascar perform algebra on tree seeds in order to tell the future?
• ... that Ewa Ligocka cooked another mathematician's goose?
• ... that Latvian-Soviet artist Karlis Johansons exhibited a skeletal tensegrity form of the Schönhardt polyhedron seven years before Erich Schönhardt's 1928 paper on its mathematics?
• ... that two members of the French parliament were killed when a delayed-action German bomb exploded in the town hall at Bapaume on 25 March 1917?
• ... that Green Day's "Wake Me Up When September Ends" became closely associated with the aftermath of Hurricane Katrina?
• ... that in 1967 two mathematicians published PhD dissertations independently disproving the same thirteen-year-old conjecture?
• ... that the word algebra is derived from an Arabic term for the surgical treatment of bonesetting?
• ... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?

Did you know...

• ... that, while the criss-cross algorithm visits all eight corners of the Klee–Minty cube when started at a worst corner, it visits only three more corners on average when started at a random corner?
• ...that in senary, all prime numbers other than 2 and 3 end in 1 or a 5?
• ...that, for all prime numbers p, the pth Perrin number is divisible by p?
• ...that it is impossible to trisect a general angle using only a ruler and a compass?
• ...that in a group of 23 people, there is a more than 50% chance that two people share a birthday?
• ...that the 1966 publication disproving Euler's sum of powers conjecture, proposed nearly 200 years earlier, consisted of only two sentences?
• ...the hyperbolic trigonometric functions of the natural logarithm can be represented by rational algebraic fractions?

Featured pictures

• 
  Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
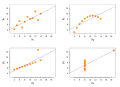
  Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals

• 

  List of all portals

• 

  The arts portal

• 

  Biography portal

• 

  Current events portal

• 

  Geography portal

• 

  History portal

• 

  Mathematics portal

• 

  Science portal

• 

  Society portal

• 

  Technology portal

• 

  Random portal

• 

  WikiProject Portals